
There are mathematical problems that seem solvable but aren’t, like squaring the circle, and others that seem impossible and yet can be solved with a little lateral thinking. Among the latter, one of the best known, and which we have already spoken about on some occasions, is that of the 9 points arranged in the shape of a 3×3 grid which must be joined with 4 straight strokes without removing the pencil from the paper and without going over the same stroke twice. And another, seen recently, is that of the obtuse triangle which must be divided into acute angles.
In the two cases mentioned, the apparent impossibility is due to the fact that, without realizing it, we impose on ourselves more conditions than those indicated in the press release. In the 9-point problem we assume that all the vertices of the broken line that joins them must coincide with some of them, which is not required of us. But what about the 4×4 grid, with how many straight lines, at least, can all the points be joined without removing the pencil from the paper or going over the same line twice? And in 5×5, 6×6…? Is there a formula that allows you to determine the number of shots based on the number of points?
As for the supposed impossibility of dividing an obtuse triangle into acute angles (Martin Gardner told me that in his time he received several “proofs” that such division was impossible), it is due to a similar false assumption: we tend to think that all the vertices of the acute angles must be on the perimeter of the obtuse angle, and this must not be the case.
Mobile card
Last week our regular commentator Salva Fuster proposed an interesting problem along the lines of the previous two (although at first glance it may seem that he has nothing to do with it, it also belongs to the family of deceivers). It is as follows:
Let’s draw a rectangle ABCD. On points A, B and C we place pieces (which form a right triangle, ABC), which can be moved. To move any one you must do it parallel to the line determined by the position of the other two pieces. How many moves are needed for two of the three pieces to be on the midpoints of two sides of the rectangle ABCD? So there are three?

Feuerbach’s point
Let’s go back to the circle of nine points. As Luis Ortiz points out: “Given that the points D, F and H are the midpoints of the segments IA, IB and IC, the triangle DFH is the result of applying a homothety to the triangle ABC, with center I and ratio 1/2. That is, DFH is a triangle similar to ABC, half the size (see corresponding figure of the previous episode). And the same homothety ratio is what the circumferences of both triangles have, including the their centers. Therefore, the center of the circumference of the nine points will be at the midpoint of the segment joining the orthocenter I with the circumcenter ABC.”
And we cannot say goodbye to the circle of nine points without mentioning the Feuerbach point, which is the point of tangency of said circle with the inscribed circle of the triangle in question.
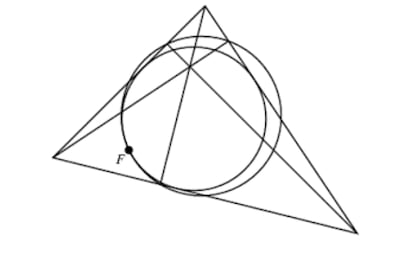
The circle of nine points, whose properties seem inexhaustible, is also tangent to the three inscribed circles (which are tangent to each side and to the extensions of the other two). Can you calculate the length of the radii of the inscribed circles of a triangle with sides 3, 4 and 5?
Finally (for now, since the topic is inexhaustible), the points of tangency of the nine-point circle with the three exinscribed circles are the vertices of the so-called Feuerbach triangle. But that’s another article.







